Bitcoin - A Peer to Peer Electronic Cash System

References

• Bitcoin: Transaction records (video) | Khan Academy
• Bitcoin: Transaction block chains (video) | Khan Academy
• The Bitcoin whitepaper, explained and commented — section 1, introduction | by Raphael M. | Medium

Introduction

Quote

Completely non-reversible transactions are not really possible, since financial institutions cannot avoid mediating disputes. The cost of mediation increases transaction costs, limiting the minimum practical transaction size and cutting off the possibility for small casual transactions.

Nakamoto was not satisfied with the current solutions for a few reasons:

• The reversibility of most transactions: trusted third parties who enable payments, are forced to play arbiters between parties when a disagreement arises, and this arbitration increases the cost of all other transactions. This cost, in turn, makes very small transaction impossible.
• On top of that, some services are simply non-reversible (for example, streaming), and thus should be paid by non-reversible transactions.

Quote

With the possibility of reversal, the need for trust spreads. Merchants must be wary of their customers, hassling them for more information than they would otherwise need.

Nakamoto is linking the reversibility of transactions to the need for merchants to “know their customers”: in other words, because transactions can be reversed, merchants have to collect more information from their customers, invading their privacy.

If payments were truly irreversible, they could occur without revealing any private information.

Quote

What is needed is an electronic payment system based on cryptographic proof instead of trust, allowing any two willing parties to transact directly with each other without the need for a trusted third party.

Here Nakamoto introduces his solution: the trust based on sharing private information with a third party can be replaced with the certainty of mathematical proofs of payment, thus eliminating the need for intermediaries.

The non-reversibility of payments will ensure that merchants are protected (buyers can’t cancel their payments), while buyers can be protected through escrow mechanisms. An escrow works by delaying payment until the goods or services have been received by the buyer.

Quote

In this paper, we propose a solution to the double-spending problem using a peer-to-peer distributed timestamp server to generate computational proof of the chronological order of transactions.

The double-spending problem: if two transactions try to spend the same virtual coins, the peers still have to decide which transaction came first (and reject the other one). And deciding which transaction comes first in a distributed system is complicated because of inherent lags: it takes times for messages to travel across the network.

Nakamoto’s solution will manage to assign a “timestamp” (a given date and time) to every transaction without using a central third party.

Transactions

Quote

We define an electronic coin as a chain of digital signatures. Each owner transfers the coin to the next by digitally signing a hash of the previous transaction and the public key of the next owner and adding these to the end of the coin. A payee can verify the signatures to verify the chain of ownership.

The idea that a coin is a chain of transactions. A transaction is nothing more than a payment.

If Alice wants to transfer a coin to Bob, she uses her private key to sign a message composed of the hash (digest) of the past transaction that gave her possession of the coin and Bob’s public key. This will produce the signature S:

$$S=sig{n}_{\text{senderPriKey}}(hash(\text{prevHash}||\text{recipientPubKey}))$$

The signature then is appended to the transaction.

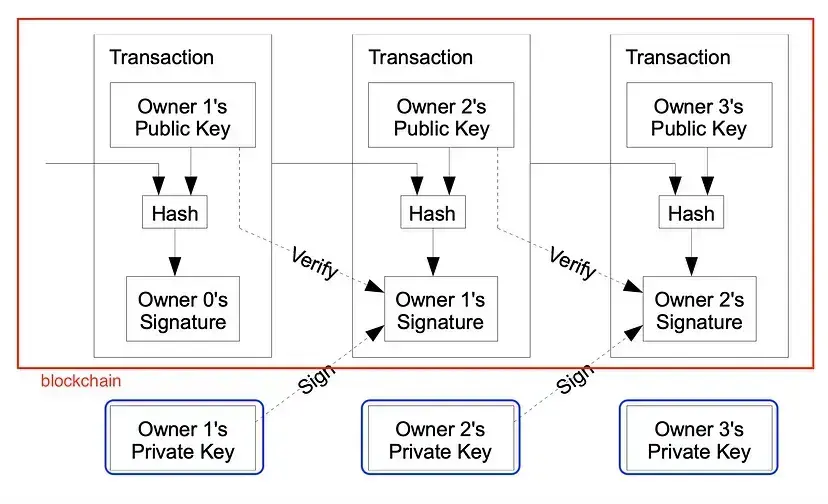
In red: information stored on the blockchain; in blue: information that each user keeps private.

The process is like this:

Quote

The problem of course is the payee can’t verify that one of the owners did not double-spend the coin.

We need a way for the payee to know that the previous owners did not sign any earlier transactions.

To accomplish this without a trusted party, transactions must be publicly announced [1], and we need a system for participants to agree on a single history of the order in which they were received. The payee needs proof that at the time of each transaction, the majority of nodes agreed it was the first received.

Here Nakamoto recognizes that, in order to solve the double-spending problems, two things have to happen:

• All transactions need to be recorded.
• There must be a way to decide, between two competing transactions (ex: trying to spend the same coin) which came first.

In order to do without a central authority, Nakamoto proposes to make all transactions public.

The new problem, however, is to make all participants agree on “a single history” of transactions (or at least a majority of participants), or in other words to agree on a particular order of transactions. But, because the system is now distributed (peer-to-peer), rather than centralized, this is not an easy task.

To solve this, Nakamoto is going to use a distributed timestamping system.

Timestamp server

Quote

The solution we propose begins with a timestamp server. A timestamp server works by taking a hash of a block of items to be timestamped and widely publishing the hash, such as in a newspaper or Usenet post.

Each timestamp includes the previous timestamp in its hash, forming a chain, with each additional timestamp reinforcing the ones before it.

• First, we group transactions that appear more or less at the same time in bundles called blocks. This is just done for efficiency: better to timestamp a bunch of non-competing transactions together than timestamp each of them individually!
• Then, we compute the hash of the transactions and publish it to an external outlet with a wide audience like a newspaper. This hash is the timestamp.
• In practice, these timestamps are computed by hashing the previous block’s timestamp together with a bunch of new transactions

The process is like this:

Proof-of-Work

Quote

Implement the proof-of-work by incrementing a nonce in the block until a value is found that gives the block’s hash the required zero bits.

So that is exactly what “miners” do in Bitcoin: they try as many nonces as possible per second and compute as many SHA-256 hashes as possible until they find a winning ticket, a hash that starts with enough leading zeros

Quote

If a majority of CPU power is controlled by honest nodes, the honest chain will grow the fastest and outpace any competing chains.

This paragraph sums up what is now called a “majority attack” or “51% attack”. This is based on the “longest chain rule”: honest nodes will always keep the blockchain that has the most proof-of-work done in it.

So, in order to forge successfully a fraudulent blockchain, the attackers must redo the proof-of-work for the block being tampered with, and all the following ones, which means they have to find winning hashes faster than the rest of the network.

Quote

To compensate for increasing hardware speed and varying interest in running nodes over time, the proof-of-work difficulty is determined by a moving average targeting an average number of blocks per hour. If they’re generated too fast, the difficulty increases.

The final piece of the puzzle is here: since participants can come and go freely (there is no authority to approve their joining and leaving), the total CPU power of the network is going to ebb and flow. That means hashes that start with a certain number of “0” are going to be found faster (when more CPUs join) or slower (when some CPUs leave).

To compensate for that, the number of “0” is adjusted dynamically so that the number of blocks found per hour remain (on average) constant. In Bitcoin, this difficulty adjustment happens every 2 weeks or so.

Network

Quote

The steps to run the network are as follows: … 4. When a node finds a proof-of-work, it broadcasts the block to all nodes. 5. Nodes accept the block only if all transactions in it are valid and not already spent. 6. Nodes express their acceptance of the block by working on creating the next block in the chain, using the hash of the accepted block as the previous hash.

In steps 4 and 5, the first miner to find a winning block hash starts spreading its solution to the rest of the network. However, since peers don’t know or trust each other, each peer has to verify that all transactions received in the winning block are indeed valid, and there is no double-spending going on.

• Even peers that don’t mine have to do that verification. In practice, despite their considerable computing power, miners are only a small percentage of the nodes of the network.
• Roles are thus quite separated: miners add transactions, while non-miners check that miners do their job correctly.
• Checking transactions and blocks only require some disk space to store the blockchain, which, as of April 2020, is around 275 GB.

From step 6, we can see it’s a virtuous circle through which honest behavior is promoted: if miners want their block accepted, they themselves have to accept only valid blocks!

Incentive

Quote

By convention, the first transaction in a block is a special transaction that starts a new coin owned by the creator of the block. This adds an incentive for nodes to support the network, and provides a way to initially distribute coins into circulation, since there is no central authority to issue them.

Each time a new block is added to the blockchain, the miner who “found” it gets new coins as a reward.

The block reward was initially 50 bitcoins, but, in order for bitcoins to reach a limited supply, rather than an ever expanding one, the reward is cut in half every 210,000 blocks (roughly 4 years).

Quote

The incentive can also be funded with transaction fees. If the output value of a transaction is less than its input value, the difference is a transaction fee that is added to the incentive value of the block containing the transaction.

With time, the block reward becomes less and less significant, decreasing the incentive for nodes to mine. To compensate for that, Nakamoto introduces a secondary incentive: transaction fees.

Quote

The incentive may help encourage nodes to stay honest. If a greedy attacker is able to assemble more CPU power than all the honest nodes, he would have to choose between using it to defraud people by stealing back his payments, or using it to generate new coins

This is where the game theory come from.

Reclaiming disk space

Quote

Once the latest transaction in a coin is buried under enough blocks, the spent transactions before it can be discarded to save disk space. To facilitate this without breaking the block’s hash, transactions are hashed in a Merkle Tree.

The term “buried under enough blocks” refers to the number of blocks that have been added to the blockchain after a particular transaction has been confirmed.

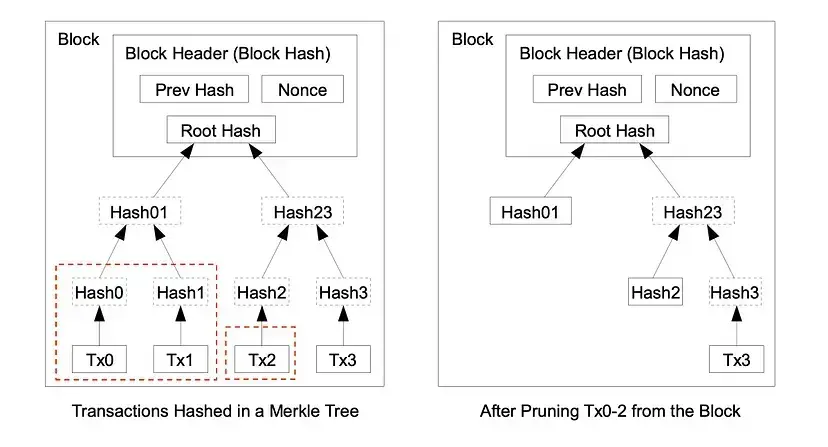
The Merkel tree of transactions is upside down, with the root on top. The transactions in the red boxes can be pruned without affecting the rest of the tree or changing the hashes.

There is no need to go into further detail here for a simple reason: Nakamoto’s idea was never implemented in the bitcoin software.

Instead, each full node of the Bitcoin network builds its own database of coins that are not spent yet. When a new transaction comes in, the node checks that this transactions only uses unspent coins, thus avoiding double-spending. Once the transaction is confirmed (when it is written in a block and added to the blockchain), the node updates its database. The unspent coins are called UTXOs, or Unspent Transaction Outputs.

A full node can decide to only keep on disk, say, the latest 50 blocks, and get rid of all the ones that came before, as long as it keeps updating the UTXO database.

Quote

A block header with no transactions would be about 80 bytes. If we suppose blocks are generated every 10 minutes, 80 bytes * 6 * 24 * 365 = 4.2MB per year. With computer systems typically selling with 2GB of RAM as of 2008, and Moore’s Law predicting current growth of 1.2GB per year, storage should not be a problem even if the block headers must be kept in memory.

In sum, it only takes about 50 MB to store 10 years of block headers.

Simplified payment verification

Simplified Payment Verification or SPV, is the method that only requires downloading the block headers (that is the metadata at the beginning of each block) but not the transactions themselves. By doing so, SPV can run with less than 100 MB of header data, instead of the current 324 GB of blockchain data (as of March 2022).

Quote

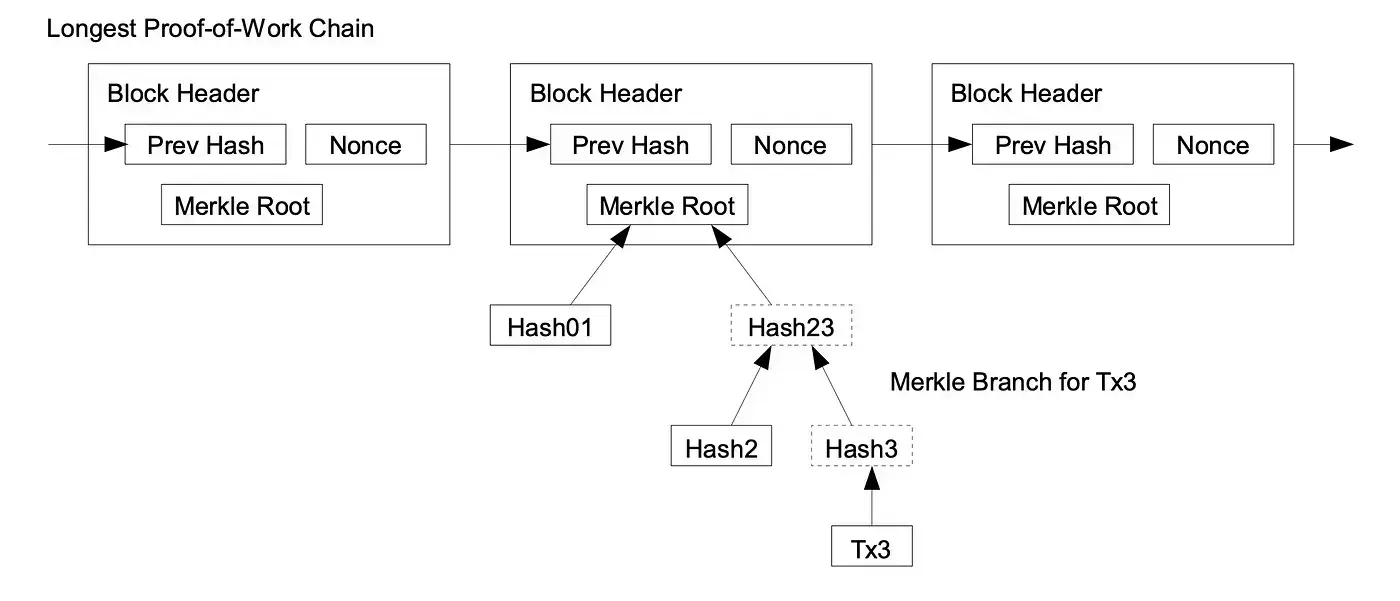
A user only needs to keep a copy of the block headers of the longest proof-of-work chain, which he can get by querying network nodes until he’s convinced he has the longest chain, and obtain the Merkle branch linking the transaction to the block it’s timestamped in.

He can’t check the transaction for himself, but by linking it to a place in the chain, he can see that a network node has accepted it, and blocks added after it further confirm the network has accepted it.

If you only have access to the block headers of the blockchain, and you want to verify that a transaction (a payment) is valid, how can you do it?

Let’s say Ben sends you a bitcoin payment and assures you that it is mined into the blockchain, say at block #300201.

How can you verify that without downloading the whole block? Thanks to the Merkle tree, you only need to download the transactions that are along the path, which is called Merkle path and can be queried from the network, of Ben’s payment in the Merkle tree.

Even if the block contains about 2,000 transactions, the Merkle tree will usually be no more than 11 or 12 levels high (2¹¹ is 2048.) That means you only need to download a dozen transactions to be able to verify Ben’s payment: you compute the hashes along the path up the pyramid starting at Ben’s payment, and you check that the hash you obtain at the top is indeed the root hash stored in the block header.

Quote

One strategy to protect against this would be to accept alerts from network nodes when they detect an invalid block, prompting the user’s software to download the full block and alerted transactions to confirm the inconsistency.

While an “invalid block” is rejected by honest full nodes in Bitcoin, a dishonest node might try to convince an SPV node to accept it. So here Satoshi suggests that light nodes should be listening for alerts about such fraudulent blocks.

Mobile wallets in reality In reality, very few mobile wallets have adopted the exact SPV scheme. Instead, they usually rely on querying trusted full nodes: they delegate the verification to nodes that they know and trust.

Combining and Splitting Value

Quote

To allow value to be split and combined, transactions contain multiple inputs and outputs. Normally there will be either a single input from a larger previous transaction or multiple inputs combining smaller amounts, and at most two outputs: one for the payment, and one returning the change, if any, back to the sender.

What Satoshi is describing here is what transactions (payments) look like.

For example, you can have the following transaction:

• Inputs: 5 BTC + 2.23 BTC + 2.1 BTC (coins that are being burned).
• Output: 8.5 BTC + 0.83 BTC (new coins that are being created).

A similar transaction is illustrated in the whitepaper: combining 3 inputs and splitting the total into 2 outputs (here a payment of 8.5 BTC for example and a change of 0.83 BTC)

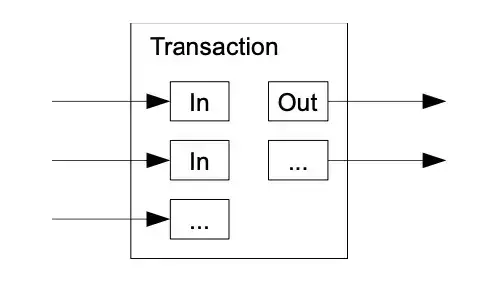
Each input and output of this transaction would be later called a UTXO, an Unpent Transaction Output. A transaction burns some UTXOs (the inputs) and creates new ones (the outputs).

In Bitcoin, if you only have a 1 BTC in your wallet and need to send a 0.1 BTC payment to your friend Alyssa, then your bitcoin would look like this:

• Inputs: 1 BTC (from your wallet).
• Output 0.1 BTC (to Alyssa) and 0.9 BTC (change back to your wallet).

Note that there is no formal difference between a payment and the change! So there is not always a way to decide, by looking at a transaction’s outputs, which ones are payments and which ones are change going back to the sender. Also, the “change” may be much bigger than the payment, as in the example above.

The UTXO database In practice, Bitcoin’s software maintains a local database of UTXOs, or Unspent Transaction Outputs. Each time a transaction is validated, its inputs are removed from the database and the outputs are added.

Quote

It should be noted that fan-out, where a transaction depends on several transactions, and those transactions depend on many more, is not a problem here. There is never the need to extract a complete standalone copy of a transaction’s history.

In other words, once you know what the UTXOs are, you don’t have to constantly dig into each one’s history to make sure a transaction is valid.

To be valid, a transaction must have all its inputs unspent, i.e. they must be in the current UTXO set before the transaction is validated. That’s how Bitcoin avoids double-spending: once an input (a coin) is spent, it disappears from the UTXO database and therefore cannot be spent again.