Keyed Permutations
AES, giống như tất cả các mật mã khối tốt, thực hiện một “hoán vị có khóa” (keyed permutation). Điều này có nghĩa là nó ánh xạ mọi khối đầu vào có thể có tới một khối đầu ra duy nhất, với một khóa xác định hoán vị nào sẽ được thực hiện.
Summary
Một “khối” chỉ đề cập đến một số bit hoặc byte cố định, có thể đại diện cho bất kỳ loại dữ liệu nào. AES xử lý một khối và xuất ra một khối khác. Chúng ta sẽ nói cụ thể về biến thể của AES hoạt động trên các khối 128 bit (16 byte) và khóa 128 bit, được gọi là AES-128.
Sử dụng cùng một khóa, hoán vị có thể được thực hiện ngược lại, ánh xạ khối đầu ra trở lại khối đầu vào ban đầu. Điều quan trọng là phải có sự tương ứng một-một giữa các khối đầu vào và đầu ra, nếu không chúng ta sẽ không thể dựa vào bản mã để giải mã trở lại cùng một bản rõ mà chúng ta đã bắt đầu.
Resisting Bruteforce
Nếu một mật mã khối an toàn, sẽ không có cách nào để kẻ tấn công phân biệt được đầu ra của AES với một hoán vị ngẫu nhiên các bit. Hơn nữa, sẽ không có cách nào tốt hơn để hoàn tác hoán vị hơn là chỉ đơn giản là bruteforce mọi khóa có thể có. Đó là lý do tại sao các học giả coi một mật mã về mặt lý thuyết là “bị phá vỡ” nếu họ có thể tìm thấy một cuộc tấn công mất ít bước hơn để thực hiện so với việc bruteforce khóa, ngay cả khi cuộc tấn công đó là không khả thi trên thực tế.
Summary
Việc bruteforce một không gian khóa 128-bit khó đến mức nào? Một người nào đó đã ước tính rằng nếu bạn sử dụng sức mạnh của toàn bộ mạng lưới khai thác Bitcoin để chống lại một khóa AES-128, sẽ mất hơn một trăm lần tuổi của vũ trụ để bẻ khóa.
Hóa ra có một cuộc tấn công vào AES tốt hơn bruteforce, nhưng chỉ một chút - nó làm giảm mức độ bảo mật của AES-128 xuống còn 126,1 bit và đã không được cải thiện trong hơn 8 năm. Với “biên độ an toàn” lớn được cung cấp bởi 128 bit và việc thiếu các cải tiến mặc dù đã được nghiên cứu rộng rãi, nó không được coi là một rủi ro đáng tin cậy đối với an ninh của AES. Nhưng vâng, theo một nghĩa rất hẹp, nó “phá vỡ” AES.
Cuối cùng, trong khi máy tính lượng tử có khả năng phá vỡ hoàn toàn các hệ thống mật mã khóa công khai phổ biến như RSA thông qua thuật toán của Shor, chúng được cho là chỉ cắt giảm một nửa mức độ bảo mật của các hệ thống mật mã đối xứng thông qua thuật toán của Grover. Đây là một lý do tại sao mọi người khuyên dùng AES-256, mặc dù nó hoạt động kém hiệu quả hơn, vì nó vẫn sẽ cung cấp một mức độ bảo mật rất đầy đủ là 128 bit trong một tương lai lượng tử.
Structure of AES
Để đạt được một hoán vị có khóa mà không thể đảo ngược nếu không có khóa, AES áp dụng một số lượng lớn các hoạt động trộn ad-hoc trên đầu vào. Điều này hoàn toàn trái ngược với các hệ thống mật mã khóa công khai như RSA, vốn dựa trên các vấn đề toán học riêng lẻ tao nhã. AES kém tao nhã hơn nhiều, nhưng nó rất nhanh.
Ở cấp độ cao, AES-128 bắt đầu với một “lịch trình khóa” (key schedule) và sau đó chạy 10 vòng trên một trạng thái. Trạng thái bắt đầu chỉ là khối bản rõ mà chúng ta muốn mã hóa, được biểu diễn dưới dạng một ma trận 4x4 byte. Trong suốt 10 vòng, trạng thái được sửa đổi liên tục bởi một số phép biến đổi khả nghịch.
Summary
Mỗi bước biến đổi có một mục đích xác định dựa trên các thuộc tính lý thuyết của các mật mã an toàn do Claude Shannon thiết lập vào những năm 1940. Chúng ta sẽ xem xét kỹ hơn từng thuộc tính này trong các thử thách sau.
Đây là tổng quan về các giai đoạn mã hóa AES:
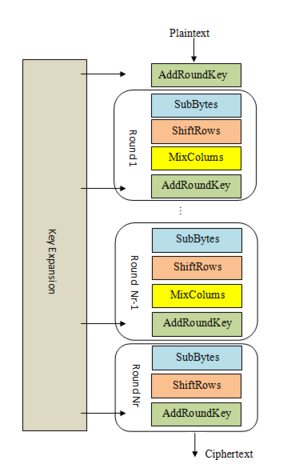
- KeyExpansion hoặc Lịch trình khóa: từ khóa 128-bit, 11 “khóa vòng” (round keys) 128 bit riêng biệt được tạo ra: một để được sử dụng trong mỗi bước AddRoundKey.
- Thêm khóa ban đầu: AddRoundKey - các byte của khóa vòng đầu tiên được XOR với các byte của trạng thái.
- Vòng - giai đoạn này được lặp lại 10 lần, cho 9 vòng chính cộng với một “vòng cuối cùng”
- SubBytes - mỗi byte của trạng thái được thay thế cho một byte khác theo một bảng tra cứu (“S-box”).
- ShiftRows - ba hàng cuối cùng của ma trận trạng thái được hoán vị — dịch chuyển qua một cột hoặc hai hoặc ba.
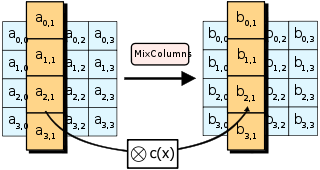
- MixColumns - phép nhân ma trận được thực hiện trên các cột của trạng thái, kết hợp bốn byte trong mỗi cột. Điều này được bỏ qua trong vòng cuối cùng.
- AddRoundKey - các byte của khóa vòng hiện tại được XOR với các byte của trạng thái.
Giải mã:
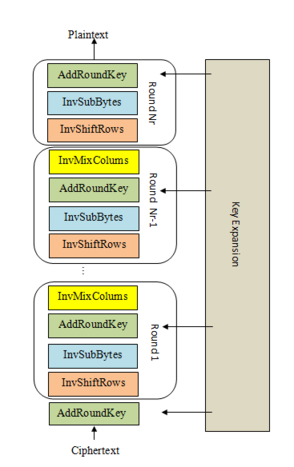
Round Keys
Chúng ta sẽ bỏ qua các chi tiết nhỏ hơn của giai đoạn KeyExpansion trong lúc này. Điểm chính là nó lấy khóa 16 byte của chúng ta và tạo ra 11 ma trận 4x4 được gọi là “khóa vòng” có nguồn gốc từ khóa ban đầu của chúng ta. Các khóa vòng này cho phép AES tận dụng tối đa khóa duy nhất mà chúng ta đã cung cấp.
Giai đoạn thêm khóa ban đầu, tiếp theo, có một bước AddRoundKey duy nhất. Bước AddRoundKey rất đơn giản: nó XOR trạng thái hiện tại với khóa vòng hiện tại.
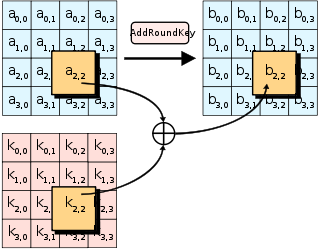
AddRoundKey cũng xảy ra như là bước cuối cùng của mỗi vòng. AddRoundKey là thứ làm cho AES trở thành một “hoán vị có khóa” chứ không chỉ là một hoán vị. Đó là phần duy nhất của AES nơi khóa được trộn vào trạng thái, nhưng nó rất quan trọng để xác định hoán vị xảy ra.
Confusion Through Substitution
Bước đầu tiên của mỗi vòng AES là SubBytes. Điều này liên quan đến việc lấy mỗi byte của ma trận trạng thái và thay thế nó cho một byte khác trong một bảng tra cứu 16x16 được đặt trước. Bảng tra cứu được gọi là “Hộp thay thế” hoặc “S-box” cho ngắn gọn, và có thể gây bối rối lúc đầu. Hãy cùng phân tích.
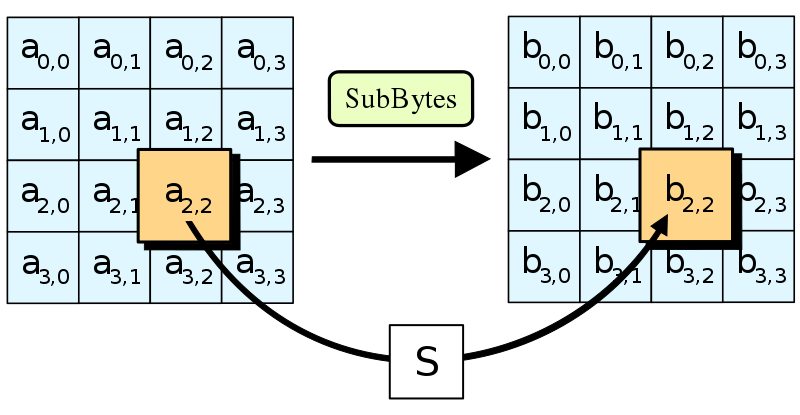
Năm 1945, nhà toán học người Mỹ Claude Shannon đã xuất bản một bài báo đột phá về Lý thuyết thông tin. Nó đã xác định “sự nhầm lẫn” (confusion) là một thuộc tính thiết yếu của một mật mã an toàn. “Sự nhầm lẫn” có nghĩa là mối quan hệ giữa bản mã và khóa phải càng phức tạp càng tốt. Chỉ với một bản mã, sẽ không có cách nào để biết bất cứ điều gì về khóa.
Nếu một mật mã có sự nhầm lẫn kém, có thể biểu diễn mối quan hệ giữa bản mã, khóa và bản rõ dưới dạng một hàm tuyến tính. Ví dụ, trong mật mã Caesar, ciphertext = plaintext + key. Đó là một mối quan hệ rõ ràng, dễ dàng đảo ngược. Các phép biến đổi tuyến tính phức tạp hơn có thể được giải quyết bằng các kỹ thuật như loại bỏ Gaussian. Ngay cả các đa thức bậc thấp, ví dụ như một phương trình như x^4 + 51x^3 + x, cũng có thể được giải quyết hiệu quả bằng các phương pháp đại số. Tuy nhiên, bậc của đa thức càng cao, nói chung nó càng trở nên khó giải quyết hơn - nó chỉ có thể được xấp xỉ bởi một lượng lớn hơn và lớn hơn các hàm tuyến tính.
Mục đích chính của S-box là biến đổi đầu vào theo cách chống lại việc bị xấp xỉ bởi các hàm tuyến tính. S-box đang hướng tới tính phi tuyến tính cao, và trong khi S-box của AES không hoàn hảo, nó khá gần. Việc tra cứu nhanh trong S-box là một lối tắt để thực hiện một hàm rất phi tuyến tính trên các byte đầu vào. Hàm này liên quan đến việc lấy nghịch đảo modular trong trường Galois 2**8 và sau đó áp dụng một phép biến đổi afin đã được tinh chỉnh để có sự nhầm lẫn tối đa. Cách đơn giản nhất để biểu diễn hàm là thông qua đa thức bậc cao sau:
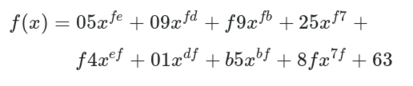
Để tạo ra S-box, hàm đã được tính toán trên tất cả các giá trị đầu vào từ 0x00 đến 0xff và các đầu ra được đặt trong bảng tra cứu.
Diffusion Through Permutation
Chúng ta đã thấy cách thay thế S-box cung cấp sự nhầm lẫn. Thuộc tính quan trọng khác được Shannon mô tả là “sự khuếch tán” (diffusion). Điều này liên quan đến cách mọi phần của đầu vào của một mật mã nên lan truyền đến mọi phần của đầu ra.
Bản thân việc thay thế tạo ra tính phi tuyến tính, tuy nhiên nó không phân phối nó trên toàn bộ trạng thái. Nếu không có sự khuếch tán, cùng một byte ở cùng một vị trí sẽ được áp dụng các phép biến đổi giống nhau trong mỗi vòng. Điều này sẽ cho phép các nhà phân tích mật mã tấn công riêng từng vị trí byte trong ma trận trạng thái. Chúng ta cần xen kẽ các phép thay thế bằng cách xáo trộn trạng thái (theo cách có thể đảo ngược) để các phép thay thế được áp dụng trên một byte ảnh hưởng đến tất cả các byte khác trong trạng thái. Mỗi đầu vào vào S-box tiếp theo sau đó trở thành một hàm của nhiều byte, có nghĩa là với mỗi vòng, độ phức tạp đại số của hệ thống tăng lên rất nhiều.
Summary
Một lượng khuếch tán lý tưởng gây ra sự thay đổi một bit trong bản rõ sẽ dẫn đến sự thay đổi về mặt thống kê một nửa số bit của bản mã. Kết quả mong muốn này được gọi là hiệu ứng thác.
Các bước ShiftRows và MixColumns kết hợp để đạt được điều này. Chúng hoạt động cùng nhau để đảm bảo mọi byte ảnh hưởng đến mọi byte khác trong trạng thái chỉ trong vòng hai vòng.
ShiftRows là phép biến đổi đơn giản nhất trong AES. Nó giữ nguyên hàng đầu tiên của ma trận trạng thái. Hàng thứ hai được dịch chuyển sang trái một cột, bao quanh. Hàng thứ ba được dịch chuyển hai cột, hàng thứ tư ba cột. Wikipedia diễn đạt rất hay: “tầm quan trọng của bước này là để tránh các cột được mã hóa độc lập, trong trường hợp đó AES sẽ thoái hóa thành bốn mật mã khối độc lập.”
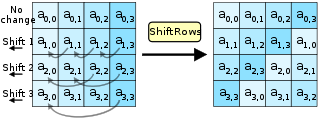
MixColumns phức tạp hơn. Nó thực hiện phép nhân ma trận trong trường Galois của Rijndael giữa các cột của ma trận trạng thái và một ma trận đặt trước. Do đó, mỗi byte đơn của mỗi cột ảnh hưởng đến tất cả các byte của cột kết quả. Các chi tiết triển khai rất tinh tế; trang này và Wikipedia đã trình bày tốt về chúng.