Bài toán Byzantine Generals Problem (BGP) nói rằng: có một nhóm các vị tướng quân cùng vây bắt một thành phố nào đó. Cuộc tấn công vào thành phố sẽ thất bại nếu chỉ có một vài vị tướng quân cùng tấn công. Nói cách khác, tất cả các vị tướng quân phải cùng tấn công vào cùng một thời điểm thì mới có thể giành chiến thắng.
Các vị tướng quân này cần liên lạc với nhau để đạt được sự thống nhất về thời gian tấn công hoặc chọn rút lui.
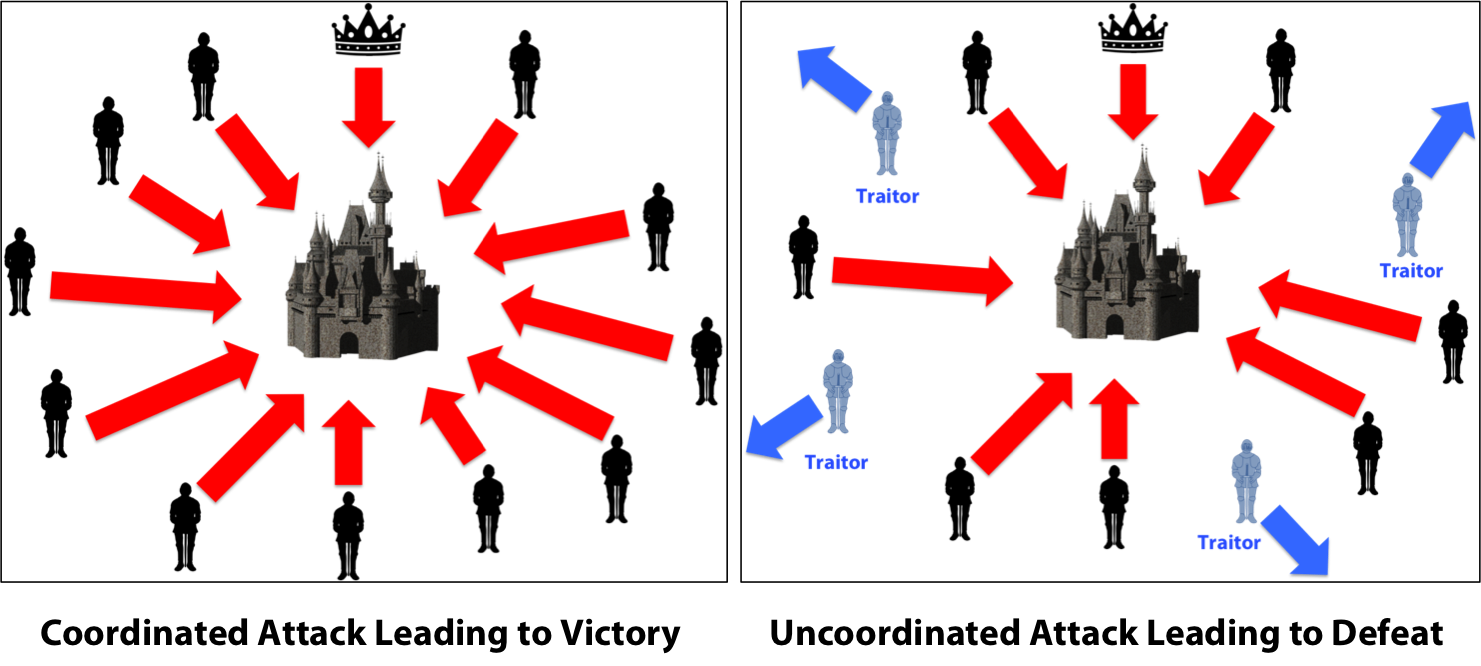
Tuy nhiên, có thể có tướng quân phản bội. Vị tướng phản bội này sẽ gửi những quyết định khác nhau đến các tướng quân khác nhau.
Giả sử có tổng cộng 6 vị tướng (ABCDEF) và 1 người phản bội. Nếu vị tướng phản bội đó gửi quyết định tấn công đến 3 người (ABC) và gửi quyết định rút lui đến 3 người khác (DEF) thì nhóm các vị tướng chọn tấn công (ABC) sẽ thất bại.
Làm sao để đạt được sự đồng thuận? Câu trả lời là cần phải dựa vào sự lựa chọn của số đông.
Một giải pháp cho bài toán này đó là: với m kẻ phản bội thì phải có ít nhất 3m số lượng tướng quân. Tức là số lượng kẻ phản bội phải không được vượt quá 1/3 tổng số lượng tướng quân. Đây cũng chính là nguyên lý hoạt động của cơ chế đồng thuận PBFT (Practical Byzantine Fault Tolerance).